ストレスと自律神経の科学

AICによるARモデルの次数決定法
自己回帰モデル（AR法）を用いたパワースペクトル密度算出　その２

「ARモデルのパラメータ推定法」では、ARモデルの次数Mを仮定した条件下で、その最適なパラメータをユールウォーカ法（最尤法）で推定する方法を解説しました。次に、ARモデルの骨格の選択、つまりARモデルの時数の決定方法を解説します。

ARモデル次数決定　赤池情報量基準（Akaike Infomation criterion, AIC）

さて、ユールウォーカ法を実行するには、あらかじめARモデルの次数Mを決定してから取りかかる必要がありました。ユールウォーカ法や最尤法は、与えられたモデルの骨格（モデルクラスとでもいいましょうか）を前提として最適なモデルパラメータを決定する手法であり、モデルクラスを決定することに相当する「ARモデルの次数をいくつにすればよいか」を判断してくれるものではありません。残念ながら、次数Mを幾つにするのが妥当であるかは自明なことではありません。

先に解説した最尤法の考え方に従うと、次数の異なるいくつかのモデルを候補として用意し、その最大対数尤度（最大尤度）を求めて、最も尤度の高いモデルを正しいモデルとして採用するのが一見妥当なように見えます。しかし、結果から言うと、モデルの次数Mが大きいほど最大対数尤度が大きくなる傾向があり、複数のモデルクラス間の比較に直接最尤法を適用すると次数の高いモデルが選択されることになり妥当な結果が得られません。

そこで登場するのが、モデルクラス間の良し悪しを比較するための指標である、赤池情報量基準（AIC）です。最尤法では対数尤度が最大になるモデルパラメータを正しいモデル（パラメータ）としました。AICは、（１４）式で計算される指標で、この指標が最も小さくなるモデルを正しモデルとする、というものです。

AIC＝－２（モデルの最大対数尤度）＋２（モデルパラメータの自由度）　（１４）

AICの第一項には、－のついた最大対数尤度があるので、最大対数尤度が大きいほどAICは小さくなりモデルとして採用されやすくなります。その一方で、第二項には、モデルパラメータ数に比例して大きくなる項が付加されているので、次数の大きなモデルは採用されにくくなります。一言でいうと、第二項は、大きな次数に対するペナルティの項と言えます。

天下り的にAICの定義式を与えると、第二項のモデル自由度に比例したペナルティなど、思いつきで決めたもののように感じられるかもしれません。しかし、（１４）式のAICの形式で、候補としたモデルが真のモデルと十分に近い場合には、モデル間の近さを適切に評価できる事が解析的に導かれます。

勿論、モデルクラス間の評価（真のモデルとの近さを計量するという意味）のための指標はAICだけでなく、多くの指標が検討されています。解析的に解くのが難しいのであまり使われていませんがTIC（竹内情報量基準）や、最もよく使われているBIC（ベイズ情報量基準）等がありますが、AICの利点は、最大対数尤度にモデルの自由度の補正項が加わっただけ、というシンプルさではないでしょうか。

AICの解析的な導出や、その他の情報量基準の解説はここでは省きます。参考文献に丁寧に書かれた解説書を紹介してありますので、モデル選択に興味をもたれた方は参考にしてください。

AICによるARモデルの次数決定の実際　（matlabのサンプルコード）

ここで実際に心拍間隔時系列データをつかって、ARモデルの選択をAICで行い、ARモデルのパラメータからパワースペクトル密度関数を計算してみます。matlabのサンプルコードも載せますので参考にしてください。Signal Processing Toolbox　と　System Identification Toolbox　に含まれる組み込み関数を使いますので、これらを持っている方は実行し確認してください。

%========================================
% Matlabを使った時系列解析
% aic, pyulear を使ったモデル選択とPSD計算
%========================================
clear
%RRI時系列データを読み込む。（等時間間隔に再サンプリング済み）
load sample4aic.mat

%AR model の次数を１から５０まで順に増やしてAICを比較する
for k=1:50
ar_m = ar(Sig(1:512),k,'yw');%yulewalker法でパラメータを決定
FPE(k) = ar_m.EstimationInfo.FPE;%FPE(Final Prediction Error)も取得できる
AIC(k) = aic(ar_m);%モデルのAICを計算
end
subplot(1,2,1);plot(AIC,'-bo');
xlabel('次数　order');ylabel('AIC');
title('ARモデルの次数とAIC')

% AICの値が最少となる次数のARモデルを選択し、パワースペクトルを描く
[order min_at] = min(AIC);
Fs =1;
%次数を指定してARモデルのパラメータを算出し、PSDまで計算する。
[yPxx,yf] = pyulear(Sig(1:512),min_at,512,Fs);
subplot(1,2,2);plot(yf,yPxx);
txt_pyulear = strcat('AR(yule-walker) PSD : AR order =',num2str(min_at));
xlabel('周波数（Hz）');ylabel('PSD（msec^2/Hz）');
title(txt_pyulear);

上記のサンプルコードが読み込んでいるデータファイルはこちらになります。sample4aic

ar(vector,order,'yw') ;vectorからARモデルパラメータを計算します。

aic(model) ;モデルのAICを計算します。

pyulear(vector,order) ;vectorからユールウォーカ法で求めたARモデルのパワースペクトルを計算します。ARモデル係数からPSDを算出する過程は、「ARモデルのPSD計算法」で解説しています。

AICによる心拍変動時系列データのARモデル次数決定

AICが最少値をとる次数のARモデルを、最もふさわしいモデルクラス（モデルの骨格）として選択する、というのが教科書的な書き方になります。しかし、実際のところ、仮定したモデルが真のモデルと十分近いところにある場合にAICによるバイアス補正（真のモデルとの近さの計測）が妥当性を持つのであって、いつでも上手くいくというものではありません。心拍変動時系列データをつかって、実際にAICによるモデル選択を行ってみます。

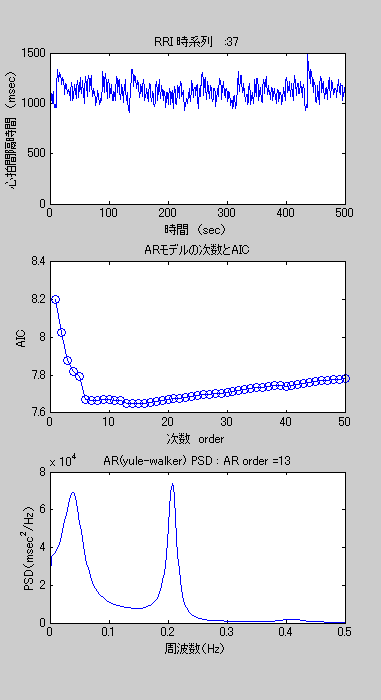
図１　心拍変動のARモデル次数選択　一例

図１に例を一つ示しました。上から元の心拍間隔（RRI）の変動時系列、ARモデルの次数を１から５０まで変化させて各モデルのAICを計算したグラフ、最もAICの値が小さいARモデル（最適な次数のARモデル）がもつパワースペクトル密度のグラフ、を順に載せています。

教科書的には、図１でしめすように、AICは次数が増えるにしたがって小さくなり、極小値をとったあとに再び増加する振る舞いをします。しかし、実際の時系列データを扱う場合、モデルの探索範囲においてAICがきれいに極小値をとるようなふるまいをするとは限りません。採用するモデルの次数が異なると、当然得られるパワースペクトルも異なり、自律神経のバランス指標であるLF,HFの値も変わってきます。この点が、ストレス指標LF/HFの計算を完全に自動的に行うことが難しい理由です。妥当なARモデルの次数決定処理を完全自動化することが一筋縄ではいかない、ということです。以下に実例をいくつか載せておきます。

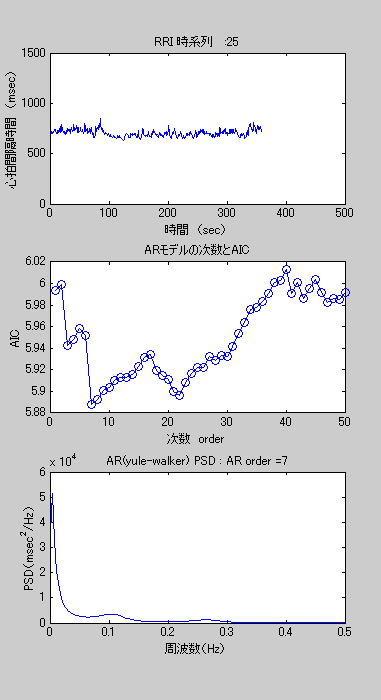
図２　心拍変動のARモデル次数選択　一例

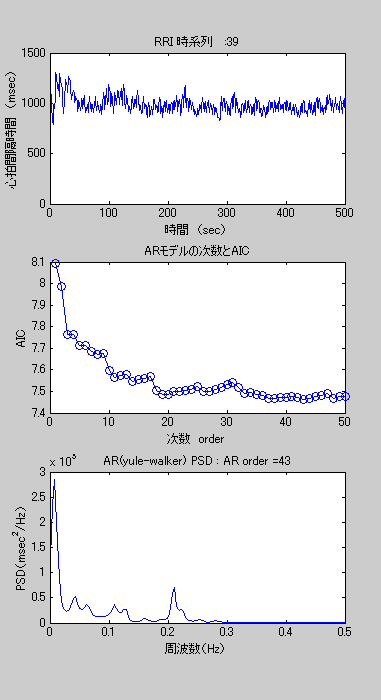
図３　心拍変動のARモデル次数選択　一例

図２のようにAICが上下変動を繰り返したり、図３のようにAICがだらだらと降下し続けるなど、判断に苦慮する例も多々でてきます。

以上で、AICによるARモデル選択の解説を締めくくります。

ARモデルの次数Mを与えた条件下で、最適なパラメータをユールウォーカ法（最尤法）で推定する方法は、「ARモデルのパラメータ推定法」を参考にしてください。

ARモデル係数からPSDを算出する過程は、「ARモデルのPSD計算法」を参考にしてください。

ストレスと自律神経の科学