パワースペクトル密度と自律神経バランス指標LF/HF

心拍変動の時系列解析に限らず、時系列データ解析においてデータの周期構造を分析するためにパワースペクトル密度は最もよくつかわれる手法の一つです。ここでは、パワースペクトルに関係する数々の概念と公式の直観的な理解ができるよう解説します。多くの教科書（参考書の紹介）に出ている定理の導出過程は記述を省略し、数式や定理が意味していることの理解を目標にします。他の分野の時系列データ解析にも使える基礎的な内容となっています。

このページで解説するパワースペクトルの計算方法はノンパラメトリック推定法と呼ばれることがあります。これに対するパラメトリック推定法は、自己回帰モデル等のように時系列データをパラーメタを持つ関数で記述しなおしてからパワースペクトルを計算する方法です。’ノンパラメトリック’の’ノン’は、少数のパラメータで記述されたモデルを用いず時系列データを直接使って議論を進めます、という意味ですので難しく考える必要はありません。

パワースペクトル密度とは（PSD；Power Spectral Densityとは）

（１）

（１）式がパワーとスペクトルに関するもっとも基本となる関係式です。まず、”パワー”とは、”信号x(t)の２乗”で定義される量です。（１）式の左辺は、時間幅を無限大まで延ばしていった時の、信号x(t)のパワーの時間平均を表しています。言い換えると、”単位時間当たりの信号x(t)のパワー”であり、時間tの単位として秒を採ると、１秒あたりの平均パワーを表わすことになります。

一方、（１）の右辺は、左辺で定義した単位時間あたりのパワーを、”周波数の世界で分析したい”という意向の表明になります。気持ちとしては、”パワー全体を、規則的な周期を持つ波にばらばらに分解してしまおう”、そして、”様々な周波数の波をすべて並べあげて、各々の周波数の波がどのくらいづつ寄与することでパワー全体を構成しているかを表現してみよう”と言った感じです。この”各々の周波数の波がパワー全体に寄与している割合を示す量”がS(ω)であり、パワースペクトル密度（PSD；Power Spectral Density）と呼ばれる量なのです。

ちなみに、ωは角速度で、周波数f(=1 / T)と比例関係にある変数でした（ω = 2 pi / T）。角速度より周波数の方が一般的になじみのある言葉と思われるので、ここでは角速度と言わずに周波数と言っておきますが、正確には角速度ωです。

（１）の段階では、意向の表明だけで、具体的なS(ω)の計算手法はまだ提示されていません。次に、S(ω)を計算する方法を検討します。

パーセバルの定理（Parsevalの定理）

ここでは、パワースペクトル密度S（ω）の実体と計算手法を知るために必要なパーセバルの公式を解説します。

（２）

（３）

S(ω)の計算方法を知るために、上記のフーリエ変換（２）式とフーリエ逆変換（３）式を使って、（１）の左辺を式変換してみます。式変形の過程は教科書類にまかせて結果を示します。

（４）

（４）式の右辺が式変形の結果になります。この（４）式に示される関係は”パーセバルの公式”と呼ばれる結果で、誤解を恐れずに平たく言うと、”単位時間あたりの信号x(t)のパワーは、信号x(t)を「直交関数の組」に分解した時の係数X(ω)の２乗の足し合わせと等しくなる”というものです。少し解説します。

直行関数の組（＝直交関数系）とは、のようにωをパラメータとした関数組のことで、”ωの値が異なる関数同士を掛け合わせて積分すると０になる”という特別な性質をもった関数組のことです。なじみのある直交関数の組としては、sin(ωt)　とか　cos(ωt)　があります。たとえばωが異なるcos(ωt)の積である、cos(ω1t)×cos(ω2t)は、適当な範囲で積分すると０になることを思い出して下さい。これが直交関数の組が持つ性質です。

直交関数の組であるに信号x(t)を分解する方法がフーリエ変換であり、（２）式に示した結果です。その分解した時の係数が、X（ω）です。そして、もとの信号x(t)は、直交関数とその係数X（ω）の足し合わせで再構成できることを示したのが（３）式であり、フーリエ逆変換なのです。

再び（４）式の右辺を見て下さい。確かに、信号x(t)を直交関数組に分解した時の各々の関数の係数であるX（ω）の２乗を、すべての周波数ωに渡って足し合わせています。そして、それが左辺で示した全パワーの合計と等しくなっていることを示しています。これがパーセバルの公式が意味するところです。

さて、パーセバルの公式を持ち出したのは、そもそも、パワースペクトル密度の計算方法を得るためでした。（４）式と（１）式を見比べて下さい。両式とも同じ左辺を持っていますので、それぞれの式の右辺同士が等しくなるはずです。そこから次の関係が得られます。

（５）

（１）式で意向の表明だけしていたパワースペクトル密度S（ω）の実体、中身が（５）式で示されるものであることがわかり、計算することができるようになりました。

（５）式を用いてパワースペクトル密度（PSD)が計算できることがわかりましたが、実際にPSDを計算する場合には、（５）から直接計算するのではなく、自己相関関数とウィナー・ヒンチンの公式を使って計算する場合が多いです。次にこれを解説します。

自己相関関数とウィーナー・ヒンチン（Wiener Khintchine）の定理

ここでは、パワースペクトル密度S（ω）を実際に算出する時に使われる、信号ｘ（ｔ）の自己相関関数と、ウィーナーヒンチンの公式の解説をします。

（６）

（６）式は、信号ｘ（ｔ）の自己相関関数の定義です。（１）式の左辺に定義された、信号ｘ（ｔ）のパワーと似た形をしていますが、すこしだけ異なっており、信号ｘ（ｔ）と、τ（タウ）だけ少し先の信号x（t+τ）を掛けたものを所定の時間範囲にわたって足し合わせています。自己相関関数は、掛け合わせる信号の時間差であるτの関数であって、時間　ｔ　の関数ではないところに注意してください。

通常、自己相関関数は、信号の周期的な構造を捉えるために利用されます。（６）式をよく観察するとわかるように、信号ｘ（ｔ）が周期T１をもつ信号なら、τがT１の倍数に近いとこで自己相関関数の値が大きくなります。

次に、（６）式を、（２）式と（３）式を使って式変形します。変形過程は省略して結果を示すと以下になります。

（７）

（７）式の右辺と、（４）式の右辺を見比べるとよく似ていてだけが異なっています。実際に、τ＝０の条件下では、は（４）式の左辺で定義したパワーと同一になるし、は１になるので、（７）式は（４）式とまったく同一になります。つまり、（４）式は、（７）式でτ＝０とした場合の特別ケースの関係式なのです。

ここで、パワースペクトル密度の実体を示した（５）式を思い出します。（７）式にも（５）式に相当する部分があるのがわかります。（５）式を使って（７）式を整理します。

（８）

（８）式は、信号x（ｔ）のパワースペクトル密度S（ω）と自己相関関数C（τ）の関係式になっています。（８）式と（３）式を比べてみると同じ形をしています。つまり、（８）式は、自己相関関数C（τ）の逆フーリエ変換になっているのです。ということは、対応するフーリエ変換もあるわけで、以下になります。

（９）

この（８）式と（９）式で示された、パワースペクトル密度S（ω）と自己相関関数C（τ）の関係式の組を、ウィーナー・ヒンチン（Wiener Khintchine）の公式と呼びます。

ウィーナー・ヒンチンの公式が示している事とご利益を確認します。まず、自己相関関数C（τ）とパワースペクトル密度S（ω）がフーリエ変換の関係にあることから、自己相関関数C（τ）とパワースペクトル密度S（ω）のもつ情報の”価値”は同じであるということです。片方が得られると自動的にもう一方も得ることができます。言いかえると、同じものを、時間と周波数という別々の側面から見ているだけだ、という事です。そして、実用上の御利益は、（９）式で示されるように、自己相関関数C（τ）を計算してフーリエ変換すると、パワースペクトル密度S（ω）が得られるという事です。

ピリオドグラム

パワースペクトル密度を計算したい場合、（５）式、もしくは、（９）式で計算すればよいことがわかりました。しかし、これらの式は、時系列データが無限に長く、連続的であるという理想的な状況での話であり、実際のデータを使ってパワースペクトル密度を算出する場合はある程度妥協する必要があります。例えば（６）式を実行しようとした場合、実際のデータで計算できる標本自己相関関数で代用することになります。その標本自己相関関数を（９）式に示すようにフーリエ変換（信号が連続でないことから、離散フーリエ変換と呼ぶ場合があります）してパワースペクトル密度を計算することになります。

理想的な（真の）パワースペクトルを、手元にある限られたデータで推定したものをピリオドグラムと呼びます。従って、（同じ確率過程から発生する、定常な）時系列データを何系列も利用できる場合、個々の時系列データから計算するピリオドグラムは互いに少しずつ異なっていますが、それらを平均していくと（直観的には）真のパワースペクトルに近づいていくわけです。（直観的には）とカッコ付きで書いたのは、厳密に言うと真のパワースペクトルに近づく性質をもっていないからです。しかし、おおざっぱには平均的な、平滑化されたスペクトルが得られます。

実用上、パワースペクトル密度を得るためには計測された実験データを利用して計算するので、”ピリオドグラムから推定されるパワースペクトル密度”などと一々言わずに、単に、”パワースペクトル密度”と呼ぶ場合が多いようです。

ピリオドグラムから推定されるパワースペクトル密度の例を示します。

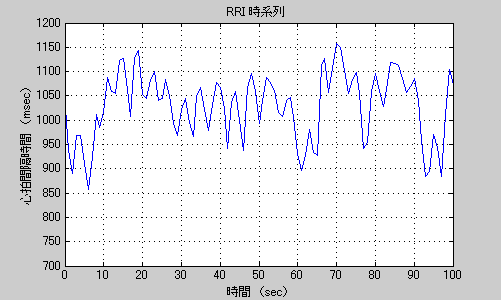
図１　心拍変動時系列データ

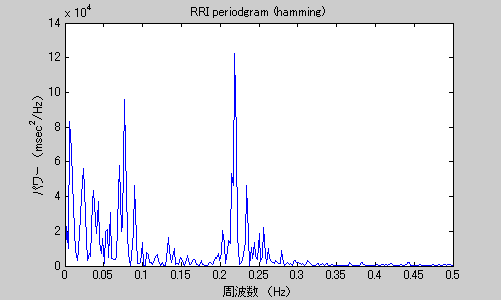
図２　ピリオドグラムから推定されるパワースペクトル密度

パワースペクトルの単位（次元）

パワースペクトル密度は、単位周波数あたりのパワーの大きさですので、その意味から直接的に、単位がであることは理解できると思いますが、もう少し丁寧に確認しておきます。

まず、自己相関関数C（τ）の次元（単位）は、（６）式の自己相関関数の定義より、Tの次元はsec、x（t）とx（t+τ）の次元はmsec、dtの次元はsecですので、結局であることがわかります。（６）式を次元について書き下すと以下のようになります。　（[単位]で次元を表わしています。あるいは、[C(τ)]の表記でC(τ)の次元を表しています。この表記法は一般的ではありませんのでご注意ください。）

となり、確かにC(τ)の次元はであると確認できます。さらに、パワースペクトル密度P(ω)の次元を（９）式より書き下します。

となり、S(ω)の単位はであると確認できました。[Hz]は[1/sec]であることに注意して下さい。