ARモデルのパラメータ推定法
自己回帰モデル(AR法)を用いたパワースペクトル密度算出 その1
少しおさらいと確認をしておきます。ストレス指標であるLF/HFは、交感神経活動と副交感神経活動のバランスを心拍変動の時系列データから計算したものでした。この自律神経バランスとしてのストレス指標を計算するためには、まず心拍変動時系列からパワースペクトル密度を算出する必要がありました。パワースペクトル密度はウィーナーヒンチンの定理を利用して自己相関関数からフーリエ変換により求める他に、自己回帰モデル(ARモデル)を利用して求めることもできます。ここではこのARモデルを利用する方法を解説します。
自律神経指標として心拍変動時系列の周波数解析をする文献では、特に断りもなく「心拍変動時系列データを自己回帰モデル(AR法)で分析すると次の式のパワースペクトルP(f)を得る」とさらりと以下の式を出します。

この式のを鵜呑みにできる方、あるいは、導出過程を理解している方は以下を読む必要はありません。ここでは、この式の導出、つまり、自己回帰モデルを利用したパワースペクトル密度の計算方法を解説します。
実際のところ、自己相関関数をフーリエ変換してパワースペクトルを得るよりも、グラフの形状が滑らかになりスペクトルの可読性が上がるためか、ARモデルを利用する方が好まれる傾向にあるようです。しかし、ストレス指標の計算を完全自動化で行うには、次数の決定というAR法に必然的に伴なう本質的な難しさがあるため注意が必要です。この本質的な問題である「次数の決定」についても、AIC(赤池情報量基準)を用いて説明します。
以下では、はじめにARモデルの説明を行います。次ぎに、得られた時系列データからARモデルのパラメータを推定するユールウォーカー法を解説します。そして、モデルの選択、つまりARモデルの次数の決定方法であるAICを説明し実例を示します。最後に、推定したARモデルのパワースペクトルを算出する上記の式を導出します。
自己回帰モデル(Autoregressive model, AR model)とは
時系列データが ![]() のように得られるとします。このデータ系列を(1)式のように、今現在の値を現在より前の値を重みづけして足し合わせ(線形和)ることで表現してみよう、というのが時系列データの自己回帰モデルです。別の表現をすると、時系列データは、(1)式に従って生成されたものとみなして、それにふさわしい(1)式のパラメータ を求めてみよう、というものです。
のように得られるとします。このデータ系列を(1)式のように、今現在の値を現在より前の値を重みづけして足し合わせ(線形和)ることで表現してみよう、というのが時系列データの自己回帰モデルです。別の表現をすると、時系列データは、(1)式に従って生成されたものとみなして、それにふさわしい(1)式のパラメータ を求めてみよう、というものです。
![]() (1)
(1)
時間sの時点でのxの値を ![]() とします。
とします。![]() はそれよりも時間jだけ過去時点でのxの値である
はそれよりも時間jだけ過去時点でのxの値である ![]() に重み
に重み ![]() を乗じた値を足し合わせたものになります。どれだけ過去のxの値の影響を考慮するかはMによって定まります。現時点からMだけさかのぼった自分自身の値の影響を受ける、とするわけです。最後の
を乗じた値を足し合わせたものになります。どれだけ過去のxの値の影響を考慮するかはMによって定まります。現時点からMだけさかのぼった自分自身の値の影響を受ける、とするわけです。最後の![]() はノイズ、とも残差とも呼ばれますが、主要項からもれた変動要素を表わす項で、どの
はノイズ、とも残差とも呼ばれますが、主要項からもれた変動要素を表わす項で、どの![]() とも無相関で、分散
とも無相関で、分散![]() の正規分布に従う確率変数であることが要求されます。
の正規分布に従う確率変数であることが要求されます。
初めて自己回帰モデルに出会う方は、自分の過去の値の線形足し合わせで現在の値を決定するモデルなど、そんな勝手な仮定をして、この世で起こる事象のいったいどれだけを表現でるのか疑問に思うのではないかと考えます。実は、工学や経済学など非常に広範囲の分野で自己回帰モデルは利用され、とくに自動制御工学の分野では重要な基礎となっています。考えてみれば、これまでに起こった現象に基づいて次の動作を決定するというのは、人間の行動においても、機械や臓器の動作においても、ある意味自然な動作設計方針と言えなくもありません。
ものは試しで、(1)式においてパラメータ![]() が与えられたとして、実験的に時系列
が与えられたとして、実験的に時系列![]() を生成してみることにします。自己回帰モデルの(1)式には確率的なふるまいをする
を生成してみることにします。自己回帰モデルの(1)式には確率的なふるまいをする![]() があるため、生成される時系列データも確率的なものとなります。
があるため、生成される時系列データも確率的なものとなります。
matlabでサンプルコードを載せますので、手元にmatlabがある方は実行して確認してみてください。(サンプルコード中で、System Identification Toolboxに含まれるidpoly,simを使っていますので、該当ツールボックスが無い場合は実行できません。)
a = [1 -1.0252 0.2142 -0.0802 -0.1071]%ar model param
m0 = idpoly(a,[])
e = iddata([],randn(400,1));
e2 = iddata([],randn(400,1));
e3 = iddata([],randn(400,1));
y = sim(m0,e);
y2 = sim(m0,e2);
y3 = sim(m0,e3);
plot(y,y2,y3)
legend('y','y2','y3',3);
title('自己回帰モデルのデータ系列生成実験')
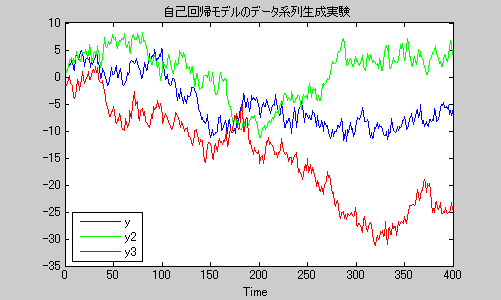
図1自己回帰モデルが生成する時系列データの例
最尤法(さいゆうほう)・尤度(ゆうど)・対数尤度(たいすうゆうど)
さて、目下の目的は、得られた時系列データ![]() を生成する元となったと考えられる(1)式の自己回帰モデルのパラメータ
を生成する元となったと考えられる(1)式の自己回帰モデルのパラメータ![]() を推定することですが、ここでは、(1)式の推定の詳細に入る前に、その際使われる推定手法である最尤法について解説します。
を推定することですが、ここでは、(1)式の推定の詳細に入る前に、その際使われる推定手法である最尤法について解説します。
前節では、自己回帰モデルのパラーメータが与えられた場合に、時系列を実験的に生成してみましたが、今度は逆に、既に得られた時系列データ![]() を生成したと思われる、最も尤(もっと)もらしい生成式(1)のパラメータは何であろうか、を考えます。今度は、未知であるパラメータ
を生成したと思われる、最も尤(もっと)もらしい生成式(1)のパラメータは何であろうか、を考えます。今度は、未知であるパラメータ![]() を手元にある時系列データから推定してみよう、という事です。確率的に生成されたデータから、それを生成した確率モデルを推定する時によく使われる基本的な考え方が、最尤法と呼ばれる考え方です。
を手元にある時系列データから推定してみよう、という事です。確率的に生成されたデータから、それを生成した確率モデルを推定する時によく使われる基本的な考え方が、最尤法と呼ばれる考え方です。
最尤法では、まずはじめに、データを生成したモデルの骨組を決めます。モデルの骨組の決定とは、たとえば、(1)式のようにM個の係数パラメータ![]() と分散パラーメタ
と分散パラーメタ![]() で記述される自己回帰モデルとする、というようなパラメータで記述される数式モデルを決めるということです。モデルの骨組の決定に王道はなく、データを生成している対象を観察し、内部で動作しているであろうモデルのあたりをつけることになります。最尤法が活躍するのは、そのモデルを前提として、もっともふさわしいパラメータの推定する場面です。
で記述される自己回帰モデルとする、というようなパラメータで記述される数式モデルを決めるということです。モデルの骨組の決定に王道はなく、データを生成している対象を観察し、内部で動作しているであろうモデルのあたりをつけることになります。最尤法が活躍するのは、そのモデルを前提として、もっともふさわしいパラメータの推定する場面です。
最尤法による(1)式のパラメータ推定は、一言で言うと次のようなものです。得られた(観測された)時系列データ![]() を生成したモデルは幾通り考えられます。そこで、考え得るいくつかのモデル候補のうち、観察されたデータを最も高い確率で生成し得たモデルを正しいモデルとしよう。そして、そのモデルでつかわれたパラーメタの値を、最も妥当な、尤(もっと)もらしい値(最尤推定値)としよう、というものです。
を生成したモデルは幾通り考えられます。そこで、考え得るいくつかのモデル候補のうち、観察されたデータを最も高い確率で生成し得たモデルを正しいモデルとしよう。そして、そのモデルでつかわれたパラーメタの値を、最も妥当な、尤(もっと)もらしい値(最尤推定値)としよう、というものです。
簡単な例をあげましょう。観察者が、ある確率分布(観察者は詳細を知らないとする)に従う確率変数から実験的に値を生成して、その実験値から最尤推定法により真の確率分布を推定するという例です。ここで取り上げるモデルは、一確率変数を生成する確率分布関数です。
xは平均0、分散1の正規分布に従う確率変数とします。図2に示す赤い点線がその確率分布の曲線で、観察者はこの確率分布は知らないものとします。ここで、確率変数xがデータを生成し、観察者は1という値を観測したとします。(図2から、xが1を生成する確率はそれなりに有り得ることがわかります。)観察者は、得られたデータであるx=1という観測値から、xが従う確率分布を推定することにします。観察者は、最尤法を使うにあたって、xを生成した確率モデルとして正規分布
![]() (2)
(2)
を仮定(ここでは、簡単のため、正規分布の分散は1であることは分かっているとします。)し、パラメータμを推定することにします。今、検討の範囲に含まれている確率モデル(仮定した正規分布というモデルの骨格)のなかで、観測データであるx=1を最も高い確率で発生させることのできる確率モデルは、μ=1の正規分布モデルであることは直観的に明らかですから、最尤法に従うと、最も妥当であろうと推定される確率モデルはμ=1の正規分布で、図2に青の実線で示される確率分布(確率モデル)になります。(x=1の発生確率が最も高くなるように、図2で正規分布のグラフを左右に移動してみると、青線のグラフが表現する正規分布の中央μ=1の時が最適であることがわかると思います。)つまり、この例で最尤法の考え方に従うと、正しい(真の)モデルの値μ=0ではなく、”間違った”値であるμ=1が推定されたという結果になります。

図2 最尤法による推定値(最尤推定値)
この例では、直観的に最尤推定値が解り易かったのですが、これを形式的に解けるようにするために、パラメータの尤(もっと)もらしさを評価するための道具として尤度(ゆうど)を導入します。尤度とは、(2)式の確率分布関数に、xの実現値であるx=1を代入してパラメータμを変数とした関数、(3)式のことです。もともと、確率分布関数は確率変数xの関数でしたが、実現値としてxが得られたので、xには実現値を代入して、未知のパラメータ(μ)を変数とする関数と見るように見方を変えたものが尤度です。この尤度を最大にするパラメータのモデルが真のモデルであると推定するのが最尤法です。すなわち、検討している範囲のモデルの中で、実現されたx=1の値を最も高い確率で生成し得たモデルを真のモデルと考えるのです。
![]() (3)
(3)
尤度関数を使って真面目に解くと、L(μ)を最大化するように(3)式の極値を求めます。
![]() (4)
(4)
(4)式を解くことで(3)式の極値が求まり、μ=1となるわけです。
さらに、尤度の対数をとったものが対数尤度です。なぜ対数をとる必要があるのか疑問に思う方もあるかと思いますが、ひとえに、対数をとると計算が楽になる場合が多いからです。(独立な確率過程の繰り返しは、尤度としては積であらわされますが、その対数をとると和としてあらわされる、等です。)また、上記の例で分かるように、尤度の利用場面は、その極値(最大化)となるパラメータ値を求める時です。極値をとるμの値は尤度でも対数尤度でも変わらないので、計算しやすい対数尤度を用いることを選択する場合が多いということです。
このように説明すると、最尤法とはかなり乱暴な推定方法のように感じたかもしれませんが、統計的推定法や統計的学習理論などの分野で様々な手法の基礎となっている有用な方法論です。
ユールウォーカー(Yule Walker)法による自己回帰モデルの係数推定
さて、いよいよ、得られた時系列データ![]() を使って、(1)式の自己回帰モデルを仮定した場合のパラメータ
を使って、(1)式の自己回帰モデルを仮定した場合のパラメータ![]() の推定値を、最尤推定法を使って求めてみます。
の推定値を、最尤推定法を使って求めてみます。
データ列を生成したモデルを(1)式の自己回帰モデルと仮定して、その最も正しそうなモデルパラメータを最尤法で推定するには、すでに得られた時系列データ![]() と、仮定した(1)式のモデルの骨格から、尤度を求めることから始めます。
と、仮定した(1)式のモデルの骨格から、尤度を求めることから始めます。
(1)式を(5)式のように変形し、![]() が分散
が分散![]() の正規分布であることに注意してさらに書き下して(6)式とします。すると、
の正規分布であることに注意してさらに書き下して(6)式とします。すると、![]() の確率分布が、時点sより前の時点のM個のデータ
の確率分布が、時点sより前の時点のM個のデータ![]() が決定した条件下での分散
が決定した条件下での分散![]() の正規分布になっていることが明確に表現されます。
の正規分布になっていることが明確に表現されます。
![]() (5)
(5)
 (6)
(6)
このように、M個のデータ![]() が与えられた条件下で、次の時点のデータ
が与えられた条件下で、次の時点のデータ![]() が発生する確率が(6)式で次々に求まります。これを
が発生する確率が(6)式で次々に求まります。これを![]() から
から![]() まで順に発生確率をすべて求めて乗算すると、時系列
まで順に発生確率をすべて求めて乗算すると、時系列![]() の発生確率になります。結局、時系列
の発生確率になります。結局、時系列![]() の発生確率は、
の発生確率は、![]() でパラメータ
でパラメータ![]() を表わすとすると、7)式のように表わされます。
を表わすとすると、7)式のように表わされます。
![]() (7)
(7)
まだ(7)式だけでは時系列の初期の部分である ![]() のデータ系列の発生確率が含まれていません。この初期のデータ系列部分に関しては、先立つM個のデータがすべてそろっていない為、(6)式で確率を表わすことができません。しかし、ここではその確率を厳密に計算せずに、計算できたとして、形式的に
のデータ系列の発生確率が含まれていません。この初期のデータ系列部分に関しては、先立つM個のデータがすべてそろっていない為、(6)式で確率を表わすことができません。しかし、ここではその確率を厳密に計算せずに、計算できたとして、形式的に ![]() のように表記しておくだけに止めます。どの道、これから解説するユールウォーカー(Yule Walker)法では、近似によりこの部分を厳密に計算することはしないからです。
のように表記しておくだけに止めます。どの道、これから解説するユールウォーカー(Yule Walker)法では、近似によりこの部分を厳密に計算することはしないからです。
ここまでの結果から、時系列データ![]() の発生確率は式(8)であることが導かれました。
の発生確率は式(8)であることが導かれました。
![]() (8)
(8)
すでに得られた時系列データ![]() の値を(8)式に代入して、パラメータ
の値を(8)式に代入して、パラメータ![]() と
と![]() の関数と見ることで(8)式は尤度関数となります。この尤度関数を最大化するパラメータ
の関数と見ることで(8)式は尤度関数となります。この尤度関数を最大化するパラメータ![]() と
と![]() が求めるべき最尤推定値になるわけです。
が求めるべき最尤推定値になるわけです。
(8)式は、厳密、正確に表記された尤度ですが、ユール・ウォーカー法では、(8)式の代わりに尤度を次のように近似的に求めます。時系列データ![]() の前後に、補助的に値が0であるダミーのデータ系列をM個づつ追加して、ダミーの系列も合わせて(6)式で発生確率を計算します。
の前後に、補助的に値が0であるダミーのデータ系列をM個づつ追加して、ダミーの系列も合わせて(6)式で発生確率を計算します。![]() をデータ系列に追加することになります。結果、(9)式を時系列データの発生確率とし、これをパラメータ
をデータ系列に追加することになります。結果、(9)式を時系列データの発生確率とし、これをパラメータ![]() と
と![]() の関数とみて、ユール・ウォーカー法による尤度とするのです。
の関数とみて、ユール・ウォーカー法による尤度とするのです。
![]() (9)
(9)
時系列の前後に無理やり0の系列を加えた近似法から想像できるように、![]() と、
と、![]() より先の系列のデータの発生確率は低く見積もられることになります。
より先の系列のデータの発生確率は低く見積もられることになります。![]() の発生確率の部分である
の発生確率の部分である![]() は無視されたと考えることもできます。しかしながら、Mに対してNが十分に大きければこのような近似も十分に成り立つと考えるわけです。
は無視されたと考えることもできます。しかしながら、Mに対してNが十分に大きければこのような近似も十分に成り立つと考えるわけです。
次のステップとして、![]() の発生確率が(6)式であることに注意して、(9)式を解析的に解きます。(6)式のようなexp関数で確率が表わされていると、尤度の対数をとると計算が楽になります。(9)式の対数をとって対数尤度を求めると、(10)式になります。(10)式では、対数尤度がパラメータ
の発生確率が(6)式であることに注意して、(9)式を解析的に解きます。(6)式のようなexp関数で確率が表わされていると、尤度の対数をとると計算が楽になります。(9)式の対数をとって対数尤度を求めると、(10)式になります。(10)式では、対数尤度がパラメータ![]() と
と![]() の関数であることを明確に示すために
の関数であることを明確に示すために![]() と表記しなおしています。
と表記しなおしています。
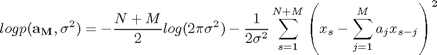 (10)
(10)
この対数尤度関数を最大化するパラメータ![]() は、(10)式を
は、(10)式を![]() のそれぞれで偏微分して=0と置いて極値を求めることで解析的に解くことができます。(10)式を
のそれぞれで偏微分して=0と置いて極値を求めることで解析的に解くことができます。(10)式を![]() で偏微分して=0とすると、
で偏微分して=0とすると、
 (10-1)
(10-1)
さらに整理して
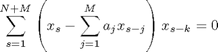 (10-2)
(10-2)
となり、k=1,2,...Mまでの![]() について同様の操作を行うことで、M個の方程式が得られることになります。これを丁寧に展開して整理すると、
について同様の操作を行うことで、M個の方程式が得られることになります。これを丁寧に展開して整理すると、
![]() (10-3)
(10-3)
![]() (10-4)
(10-4)
となります。![]() が自己相関関数(自己共分散関数)
が自己相関関数(自己共分散関数)![]() であることから、
であることから、
![]() (10-5)
(10-5)
で表現されるk個の![]() についての連立方程式が得られます。この連立方程式を行列式で見通し良く書くと(11)式になります。この連立方程式がユール・ウォーカー方程式と呼ばれるものです。
についての連立方程式が得られます。この連立方程式を行列式で見通し良く書くと(11)式になります。この連立方程式がユール・ウォーカー方程式と呼ばれるものです。
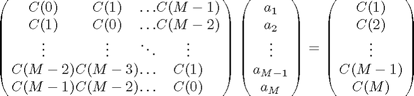 (11)
(11)
時系列データ![]() から自己相関関数を計算して、(11)式のユールウォーカー方程式を解くことで、パラメータ
から自己相関関数を計算して、(11)式のユールウォーカー方程式を解くことで、パラメータ![]() の最尤推定値が求まることがわかりました。この解である最尤推定値を
の最尤推定値が求まることがわかりました。この解である最尤推定値を![]() と通常表記します。
と通常表記します。
対数尤度関数(10)式は、パラメータ![]() の関数でもあるので、
の関数でもあるので、![]() について行った操作と同じようにして、最尤推定値を求めることができます。10式を
について行った操作と同じようにして、最尤推定値を求めることができます。10式を![]() について偏微分して=0と置いて解析的にときます。
について偏微分して=0と置いて解析的にときます。

![]() について整理すると
について整理すると
 (12)
(12)
となり、12式に![]() の最尤推定値である
の最尤推定値である![]() を代入して、
を代入して、![]() の最尤推定値である
の最尤推定値である![]() が得られます。
が得られます。
ここまでをまとめると、計測された時系列データ![]() をARモデル(1)式で記述しようとした。計測された時系列データをよく再現できる(1)の最適なパラメータを推定する必要があり、ユールウォーカ法を使った最尤推定により、近似の範囲で最適なパラメータ
をARモデル(1)式で記述しようとした。計測された時系列データをよく再現できる(1)の最適なパラメータを推定する必要があり、ユールウォーカ法を使った最尤推定により、近似の範囲で最適なパラメータ![]() と
と![]() を(11)式と(12)式により得た。
を(11)式と(12)式により得た。
ここまでで、解説は一区切りつくのですが、次に使うこともあり、最大化しようとした対数尤度(10)の最大値を計算しておきます。これは、最尤推定値である![]() と
と![]() を(10)式に代入し、(12)式を使って整理するだけです。
を(10)式に代入し、(12)式を使って整理するだけです。
![]() (13)
(13)
13式が最大対数尤度と呼ばれるものです。
次は、ARモデルの骨格の選択、「AICによるARモデルの次数決定法」を解説します。