ストレス指標としての自律神経機能活性度 その1
心拍変動時系列データからの周期情報抽出
心拍変動から自律神経のバランスを推定するために、心拍変動の時系列データから呼吸に対応する変動波と血圧変化に対応する変動波を抽出する必要があります。理工学系過程を修めた人であれば、時系列データから周期構造を抽出する、と言えば説明は不要と思いますが、そうでない人の為に、複数の周期的な波の重ね合わせによる時系列データの合成と、時系列データの周期的な波の組への分解について直観的な理解ができるように解説をしておきます。
周期性をもつ波の重ね合わせによる合成波の生成
2つの周期的に変化する時系列データを作成します。
![]()
![]()
y1は周期10秒をもつ波(Sin波)です。y2は周期1秒をもつ波ですが、こちらは振幅(振れ幅)が0.2と小さく設定します。それぞれをグラフにしてみます。
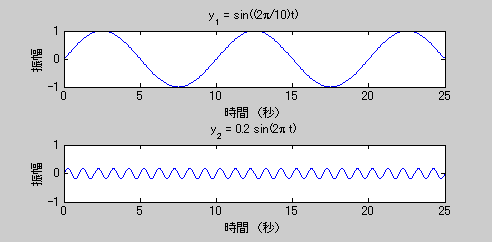
この二つの波を足し合わせて一つの波を合成してみます。Y1とY2を単純に足し合わせるだけです。
![]()
この合成した波をグラフにしてみます。周期の長い波であるY1に、振幅が小さく周期の短い波Y2が乗っている状態が視覚的に理解できると思います。
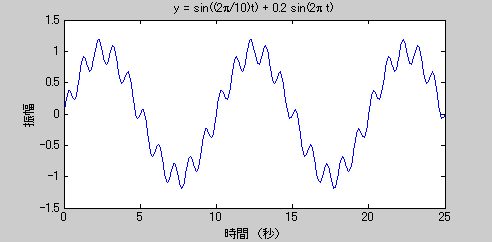
2つの別々の周期をもった波を足し合わせて複雑な合成波をつくること過程が理解できたと思います。
時系列データの周期関数組への分解 ~パワースペクトル密度(PSD)~
次に、時系列データを周期的な波の組に分解する過程を解説します。上の合成の過程と逆に、複雑な波をそれを構成する複数の周期的な波に分解することに相当します。
上の例を引き続き利用します。Yの合成波は、今さっき人工的にY1とY2を足し合わせて作ったので、振幅が1で周期が10秒の波と、振幅が0.2で周期が1秒の波から構成されていることは分かっています。これを下にグラフで明示しておきます。グラフでは、重み(振幅)が0.2で周期が1秒(周波数で言うと1Hz)の波と、重み(振幅)が1で周期が10秒(周波数で言うと0.1Hz)の波が混ざり合っている事を表現してあります。このグラフがYを構成している周期的な波の組を示した”正解”です。
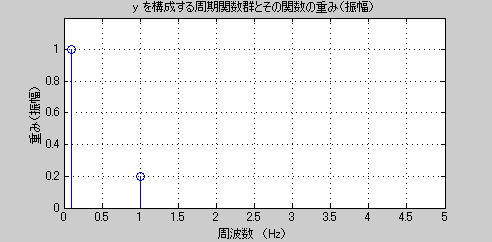
では、YがY1とY2を足し合わせて出来ていることをあらかじめ知らない場合に、Yを上のように周期的な波の組に分解することができるでしょうか?答えは、”ある程度の正確さで可能”です。与えられた時系列データを分解してその中に含まれている周期的な成分の構成比率を計算する手法は複数知られていますが、一般総称として周波数解析とかスペクトル解析等と呼ばれています。ここではもっとも広くつかわれているフーリエ変換を用いた方法をYに適用してみます。YがY1とY2で構成されているという答えは知らないとして、YからY1とY2に相当する構成要素を見つけることが出来るか確かめてみよう、というわけです。
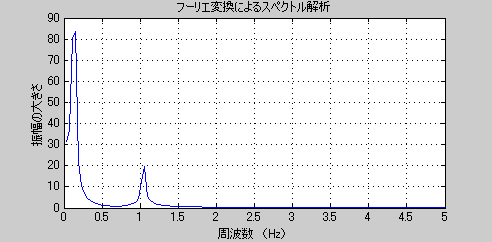
上に示した図は、Yに対して周波数解析(フーリエ展開)を実行した結果です。先ほどの図を比べてみると似ているところと異なっているところがあることに気がつくはずです。まずグラフの見方を説明します。こちらのグラフはひとつ前のグラフと異なり、連続的に示されています。周波数解析では、少しづつ異なる周波数の波がどのくらいの割合(振幅の大きさ)で混ざり合っているかを計算していくため、真の答えである1Hzと0.1Hzに近い周波数の波もいくらか混ざっていると計算の結果判断しているのです。つまり、ぴったり正解の1Hzと0.1Hzの2つの波を抽出できるわけではなく、大体、1Hz近辺の波と0.1Hz近辺の波が混合している事が見いだせるわけです。
上の図に示した、解析の結果導かれた周波数ですが、多少ずれてはいますが、大体1Hz(周期1秒)と0.1Hz(周期10秒)のピークが抽出されています。また、それぞれの強度ですが、0.1Hzと1Hzのそれぞれの周辺の周波数領域を足し合わせると、大体5:1になっているように見えます。このように、任意の時系列データに対して周波数解析を実行することによって、完全正確に元の周期関数を再現することはできませんが、おおよその構成比率を推定することができるのが理解できたと思います。
次に、もうひとつ時系列データから周期的な波の組を抽出し表現する手法であるパワースペクトルを紹介します。上で紹介した周波数解析の方法と得られる情報はほぼ同等のものですが、こちらのほうが一般的によく使われています。
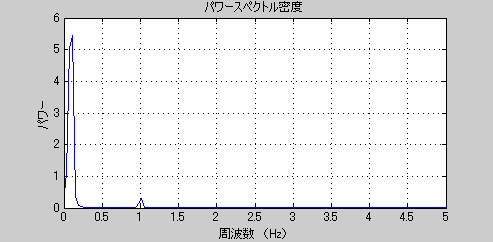
先ほどのフーリエ変換によるスペクトル解析のグラフと同様に、周波数1Hz(周期1秒)と周波数0.1Hz(周期10秒)のピークが抽出されているのが確認できます。縦軸に”パワー”をとっています。”パワー”はなじみの無い量だと思いますので簡単に説明しますと、振幅の2乗に相当する量で、振幅の比が5:1ならば、パワーの比は25:1になります。ここではパワーの意味を正確に理解しなくとも、”解析の元データを構成している各周波数の波の組成割合を表す量”、であると思ってもらえばとりあえず十分です。
さて、心拍変動の時系列データに対して、この周波数解析を実行することで、心拍間隔時系列データに潜んでいる周期関数を抽出することが次のステップになります。