心拍変動時系列とストレス指標の実際
生理機能検査実験、心理実験、自動車走行による疲労実験など、自律神経のバランスやストレス度の計測場面は多くあります。実験条件をある程度均一にコントロールできる生理機能検査実験では、心拍変動から算出されるストレス指標(LF/HF)は、イレギュラーな値を頻繁に出さないという意味において、比較的安定的に得ることができます。しかし、日常生活を自由に過ごしてもらいながら常時連続的にストレス指標を算出する場合、LF/HFの値は比較的大きく変動し何を計測しているか分からない場合も多々あります。
ストレスの計測場面:生理検査実験/日常生活
ここでは、自由行動下で、つまり、日常生活を自由に過ごしてもらいながらストレス指標を計測した場合の実例をいくつか示すことで、ストレス指標の実際の感触をつかんでもらいたいと思います。ここで計測の対象となった被験者は健康な20代男性です。
ストレス指標であるLF/HF,LF,HFを計算するためのパワースペクトル密度算出を、ピリオドグラムによる方法と自己回帰モデル(ARモデル;ユールウォーカー法)による方法の2種類について実行し、両者を比べることで手法間の違いを確認できるようにしてみました。個々のサンプルで両者に違いがでるのは当然ですが、概ね同じような傾向にあることは理解できると思います。実際に利用する際は、実装の容易さ等の因子も考慮してどちらのストレス指標計算法を採用するか判断することになります。
ストレス状態
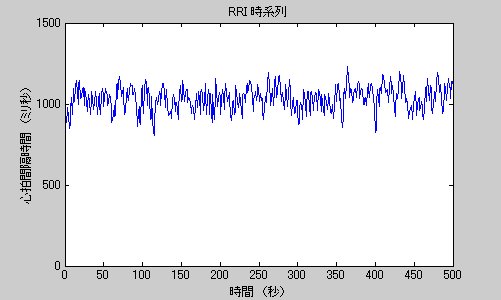
図1 ストレス状態の心拍変動
図1の心拍変動は仕事中のもので、ストレスのかかっている状態、つまり精神負荷の状態にあると考えられます。
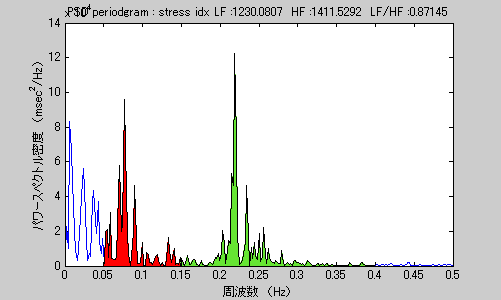
図2 ストレス状態のパワースペクトル(ピリオドグラム)
図1に示した心拍変動から算出したのパワースペクトルです。このパワースペクトルは信号を離散フーリエ変換して得られたもの(ピリオドグラム)です。
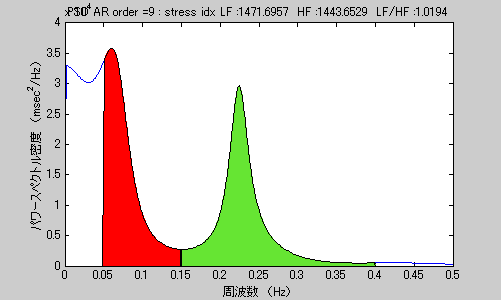
図3 ストレス時のパワースペクトル(AR法)
図1に示した心拍変動からAR法により算出したパワースペクトルです。自律神経のバランス指標であるLFとHFも同時に計算してありますが、LF/HFは約1.02という値になっています。
仕事中ということで、それなりのストレスがかかっているはずですが、比較的大きな呼吸成分(HF)が現れていることから、副交感神経(心臓迷走神経)も十分に緊張状態にあるようです。ストレスがかかっていると周りが思っている状態でも被験者はストレスを感じていないのかもしれません。(仕事にストレスを感じていないのかもしれませんね)
リラックス状態

図4 リラックス状態の心拍変動
少々極端な例を示しますが、図4は睡眠中の心拍変動のデータです。図1とくらべても変動の幅が大きく、一貫した周期構造を持っているように見えます。

図5 リラックス状態の心拍変動(拡大)
図5は、図4を拡大したものです。明確な周期構造があることがわかります。睡眠中ということで、副交感神経が最も緊張している状態であると考えられ、呼吸に合わせて心拍が大きく揺らいでいるのがわかります。

図6 リラックス状態のパワースペクトル(ピリオドグラム)
パワースペクトルも非常にシャープなピークを検出しています。

図7 リラックス状態のパワースペクトル(AR法)
図4で示した心拍変動時系列からAR法でパワースペクトルを計算し、ストレス指標を算出したものです。自律神経のバランスも明確な副交感神経亢進状態にあることを示しています。ストレス指標(LF/HF)も0.17となっており、先の例とくらべても小さな数値になっています。
運動

図8 運動時の心拍変動
図8は運動時の心拍変動時系列です。図1及び図4と比べて数秒程度の時間スケールでは心拍変動の大きさが極端に小さくなっているのが確認できます。(グラフの縦軸のスケールは変わっていません。)日常生活の自由行動下では生理機能実験のように一定の運動が継続していることはあまりありませんので、身体への負荷の変化によって心拍数はトレンドを持って変化するのが普通です。

図9 運動時のパワースペクトル(ピリオドグラム)

図10 運動時のパワースペクトル(AR法)
図9、図10は図8の心拍変動時系列のパワースペクトルです。低周波の部分にピークが集中しており、HF成分やLF成分がほとんど確認できません。
運動による身体への負荷が変わることによって、心拍数がトレンドを持って変化する場面は自由行動下の計測において非常に多く見られ、むしろ支配的であると言えます。身体運動の変化を伴う場面でのパワースペクトルには運動自体が持つ周期構造がパワースペクトルのLF成分の付近に現れるため、交感神経と副交感神経のバランスを計測しているとは言い難くなります。つまり、LFを過大に見積もってしまうことになります。
実用的な方法として、加速度センサーやジャイロセンサー等の身体運動を検出するためのセンサーを併用して、運動が変則的に変化している場面では、LF/HFのストレス指標を外れ値として捨てる等の対策をとることが有効です。
加齢・疾患による心拍変動の変化傾向
心拍変動の大きさには個人差があります。また、一般的に、加齢によって心拍変動は小さくなる傾向があります。さらに、糖尿病、高血圧、心筋梗塞などの心臓疾患によって心拍変動が著しく小さくなる場合があります。心臓疾患後の経過が良好か不良かを推定するために心拍変動が重要な指標になることが様々な研究で指摘されています。心拍変動の臨床応用については”書籍の紹介”を参考にしてください。
生活習慣病(糖尿病)の診断を受けている別の被験者(50代男性)の例を示します。くつろいでテレビを視聴していた時の心拍変動で、表面的観察の視点からはストレスを感じることもなくリラックスしていると言える状態です。

図11 (加齢・疾患)リラックス状態の心拍変動
先の被験者の心拍変動に比べてかなり心拍変動が少ないことが確認できます。身体運動負荷が無いことも心拍のトレンドが平坦であることから確認できます。

図12 (加齢・疾患)リラックス状態のパワースペクトル(ピリオドグラム)

図13 (加齢・疾患)リラックス状態のパワースペクトル(AR法)
図11のパワースペクトルです。パワー自体も先の被験者と比べて小さく、さらに副交感神経の活性度を示すHF成分もLF成分にくらべて低めに出ています。ストレス指標(LF/HF)も2.44と比較的大きく出ており、交感神経優位の状態にあると判定できますが、疾患をもつ被験者の場合、心拍変動の減少が自律神経機能の低下によるものなのか、その他の器官の機能低下によるものなのか慎重に判断する必要があります。そのため、ストレス指標(LF/HF)のみで、交感神経が活性化していて副交感神経が不活性化している、とは一概に言えません。
ストレス指標計算のサンプルコード
自律神経のバランス指標であるLF/HFを計算するmatlabのサンプルコードを参考のため掲載します。ピリオドグラムを用いた指標の計算部分です。サンプルデータはこちらのものを利用して下さい。
%========================================
% Matlabを使った時系列解析
% 自律神経バランス指標 LF/HFの計算
%========================================
clear
%RRI時系列データを読み込む。(等時間間隔に再サンプリング済み)
load sample4aic.mat
% LF HF として積算する周波数帯域を指定
LF_low = 0.05;
LF_hi = 0.15;
HF_low = 0.15;
HF_hi = 0.40;
%
Fs = 1;
[Pxx,f] = periodogram(Sig(1:512),hamming(512),512,Fs,'onesided');%Signal Processing Toolboxが必要
delta_f = 1/2 * 1/length(f);
pow_LF = sum(Pxx .* ((LF_low < f) & (f < LF_hi))) * delta_f;
pow_HF = sum(Pxx .* ((HF_low < f) & (f < HF_hi))) * delta_f;
LFHF = pow_LF / pow_HF;
LFHFtitle = strcat('PSD periodgram : stress idx LF :',num2str(pow_LF),' HF :',num2str(pow_HF),' LF/HF :',num2str(LFHF));
Pxx_LF = Pxx .* ((LF_low < f) & (f < LF_hi));
Pxx_HF = Pxx .* ((HF_low < f) & (f < HF_hi));
set(gcf, 'Position', [100 100 500 300]);
plot(f,Pxx)
hold on
area(f,Pxx_LF,'FaceColor',[1 0 0])
area(f,Pxx_HF,'FaceColor',[.4 .9 .2])
xlabel('周波数 (Hz)')
ylabel('パワースペクトル密度 (msec^2/Hz)')
title(LFHFtitle);
hold off